Why do Scale Free Networks appear so often?

Networks (graphs in mathematics) are a collection of vertices and a collection of edges - the edges connect pairs of vertices. They are an extremely useful way of probing large electronic data sets which have become widely available over the last few years. For instance the nodes can be web pages and the edges are web links, or the nodes can be Facebook users and the edges represent connections between them. They are a key part of the "digital humanities" revolution. Some of the most significant contributions came from physicists and computer scientists around in 1999 as they pointed out that many of these data sets had non-Poissonian distributions. In particular, if you ask what is the probability that a vertex is attached to k edges (this is called degree distribution) we often find this is a very fat-tailed distribution. Sometimes these are well approximated by a power law and these became known as "scale-free networks". The model proposed at that time for the formation of such networks (Barabasi and Albert 1999) emphasised growth and a rich-get-richer principle of Price (1965) and others. That is the probability of adding a new edge to a vertex is proportional to the number of edges that vertex has, its degree k.

The growth aspect is not relevant to the existence of a power law. Non-growing networks can be found with similar fat-tails. See my work on network rewiring for more discussion on this topic.

Such simple models are badly flawed as practical models for two reasons. First they require global information. That is to normalise such distributions you must know the total number of edges. Secondly, to get power laws, the probability must be linear in the degree; any other power produces other quite different results. In reality, when writing a web site and adding new links, one neither knows nor cares how many links are in the whole web (normalisation) nor do we pick our links precisely in proportion to the degree of other sites. The challenge remained to explain why so many long tailed distributions appeared in real data sets.

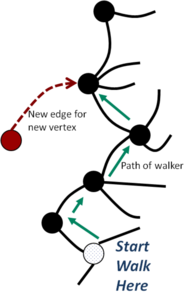
With Jari Saramäki from Aalto University in Finland I have worked on more realistic models for the formation of scale-free networks (Phys.Rev.E 72 (2005) 26138, cond-mat/0411390). The key idea is that people who construct these networks perform searches of their neighbouring network to find new connections. For instance when writing a web page you click on a web site, then follow a link from that to a new page, and then from there you click on another link, and so on. Eventually, after a few clicks, you find something of interest and you add a new link from your new web page to the one you have found. This is a "random walk" by users and it is performed using local information only - you only use what you find see on nearby web pages. You do not need to know the whole network (which would be global knowledge). It is an example of what is now known as `social computing'. Most simple algorithms, including the original one of Barabasi and Albert, use global information, often hiding in the normalisation of their probabilities. Our theoretical approximations showed that long random walks will produce an effective attachment probability proportional to the degree k. Thus the rich-get-richer (preferential attachment) probability discussed in the literature emerges from the dynamics of the system. Our numerical results showed that for any type of random walk, even for single step walks, a wide-tailed distribution is produced which are well fitted by power laws. What changes with different types of walk is the width of the distribution (the value of the power). Thus we explained both the existence of such power-law distributions and, just as important, the lack of a universal value for these powers. Such universality is a key signal of what is known as critical behaviour and self-organised criticality. There had been suggestions that this might be behind the power laws but but had this had not been seen in the data sets, and our model explains why. So I believe that the many long tailed distributions seen in real in networks are created because some sort of local search is being used in their creation. The random walk in our simple models captures the essential behaviour, at least in a statistical sense.

(click on image for larger version)

Further sources

This is a talk on this topic entitled Scale Free Networks from Self Organisation which I gave at the 5th meeting in the Mathematics of Networks series, held in Oxford on 7th April 2006.

Also see the talks Are Copying and Innovation Enough? (Brunel University Complexity Community, 2007) and Randomness and Complexity in Networks (Pisa, 2007) as well as proceedings for the latter [arXiv:0711.0603]. These put this work into the broader context of copying and inheritance. A talk entitled Random Walks and Networks given in USP, Sao Paulo in December 2011 puts this work in the wider context of the use of random walks in network analysis.