(Click on image for larger version)
| Tim Evans Informal Home Page | Tim Evans Imperial College page |
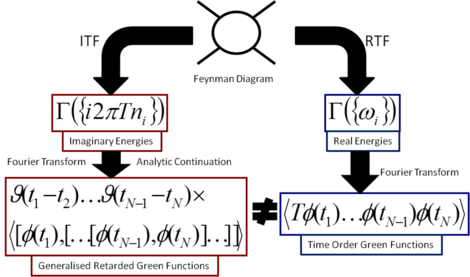
There are two distinct approaches to calculations in Thermal Field Theory. One is based on the use of real physical times, called RTF (Real Time Formalism). The other uses unphysical imaginary times, the Matsubara formalism or ITF (Imaginary Time Formalism). ITF is the older, apparently simpler (its not underneath the surface) and more popular approach. The question is how do you reach physical quantities describing dynamics, such as the propagation or interaction of physical particles? Technically, how do you calculate Green functions at real (physical) times?
As RTF is constructed using real times it produces the desired results directly. With the ITF method, one has to perform an analytic continuation of results of its calculations as everything in ITF is expressed in imaginary time. What I showed in N-Point Finite Temperature Expectation Values at Real Times was that while the terms of the calculations in RTF and ITF match, that is the same Feynman diagrams are involved, the results are very different. This had been shown in one simple explicit example before but the reasons for the difference had not been understood. In this paper I not only showed that this mismatch was not a mistake but that it was a general feature. In particular I showed that the analytic continuation of ITF to real times produced different types of real-time Green function (retarded and generalised retarded Green functions) from those obtained in RTF (time-ordered Green functions). Thus the two methods calculate the same dynamical physics but they wrap up the physics in two different forms. I also provided a way to relate the results from the two calculational formalisms. Surprisingly, this relationship was well known for simple propagation (two-point Green functions) but had not been understood in more general cases. My work applied to practical calculations and to the general case.
As part of this work I defined a new sequence of integers, 2, 6, 32, 370, 11292, 1066044, 347326352, 419172756930, etc., which is Sloane sequence A034997 (see also What is being calculated with Thermal Field Theory?). This sequence has since been revisited using different techniques.
The case for three-point functions is the simple yet illustrates many of the main points. This was developed in an earlier paper
3-Point Functions at Finite Temperature in Phys. Lett. B 249 (1990) 286-290. The work also shows how to construct spectral representations of higher-order Green functions in thermal field theory. Again the three-point case is the simplest and was developed in another paper Spectral Representation of Three Point Functions at Finite Temperature Phys. Lett. B 252 (1990) 108-112.

(Click on image for larger version)
Wick's Theorem in Thermal Field Theory
Another aspect of my work on formal aspects has been to look at Wick's theorem in thermal field theory. This is central to the canonical approach to any Quantum Field Theory (usually it is the first method taught) yet to use it in Thermal Field Theory requires a fundamental change in the definition of normal ordering, see Wick's Theorem at Finite Temperature Nucl.Phys. B 474 (1996) 481-496 [hep-ph/9601268].